Cálculo del Momento de una Fuerza en una Viga

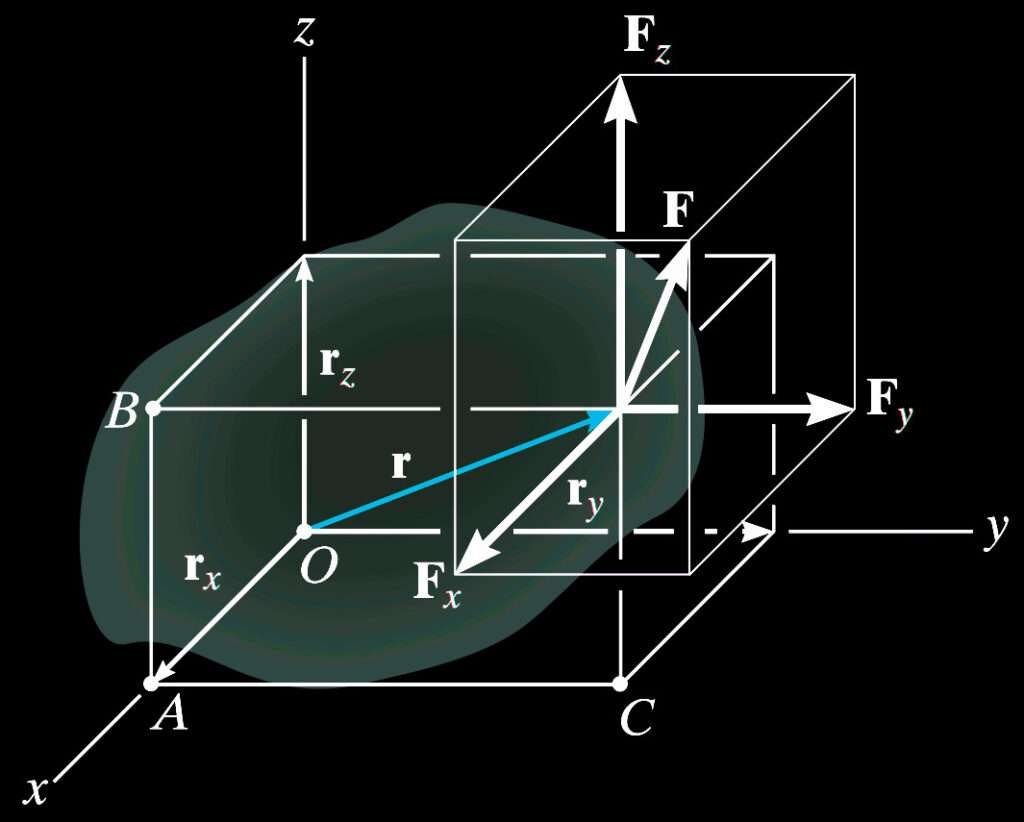
Diagrama en R3 que muestra el cálculo del momento de una fuerza en 3D utilizando el producto vectorial, con componentes de la fuerza y la posición en los ejes x, y, z.

En este artículo, vamos a resolver un problema clásico de estática, donde calculamos el momento de una fuerza con respecto a un punto dado. Este tipo de ejercicios es fundamental en la mecánica de sólidos y se aplica en el análisis estructural de vigas y otros elementos sometidos a fuerzas.

Planteamiento del Problema

La fuerza $\vec{F} = 600 \hat{i} + 300 \hat{j} - 600 \hat{k} \, N$ actúa en el extremo de una viga en el espacio tridimensional. Debemos calcular el momento de la fuerza con respecto al punto $A(0, 0, 0.4)$ . Este tipo de problemas se resuelve aplicando el producto vectorial entre el vector posición y la fuerza aplicada.

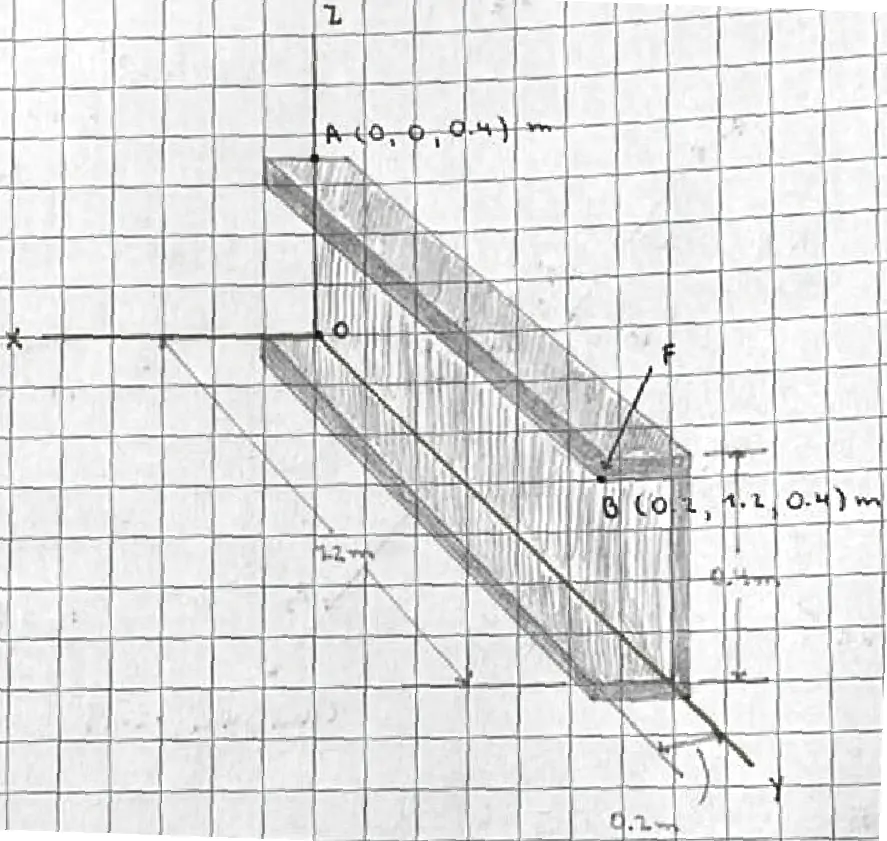
Diagrama de la viga con fuerzas aplicadas y ejes coordenados — Figura 1: Diagrama de la viga con ejes coordenados y fuerzas aplicadas.

Cálculo del Momento de la Fuerza

El primer paso es determinar el vector de posición entre los puntos $A(0, 0, 0.4)$ y $B(0.2, 1.2, 0.4)$ .

El vector posición es: $\vec{r}_{AB} = (0.2 \hat{i} + 1.2 \hat{j}) \, m$ .

Ahora, calculamos el producto cruzado entre $\vec{r}_{AB}$ y $\vec{F}$ :

$\vec{M}_A = \vec{r}_{AB} \times \vec{F} = (-720 \hat{i} + 120 \hat{j} - 660 \hat{k}) \, N \cdot m$

Así, el momento de la fuerza con respecto al punto $A$ es $\vec{M}_A = (-720 \hat{i} + 120 \hat{j} - 660 \hat{k}) \, N \cdot m$ .

Interpretación y Aplicación

El resultado obtenido es importante en el análisis estructural, ya que nos permite conocer la tendencia de rotación que produce una fuerza aplicada en una estructura. Este ejercicio es muy común en cursos de mecánica de sólidos y es fundamental para comprender cómo las fuerzas afectan a las estructuras.

Cálculo del Momento de la Fuerza

El primer paso es determinar el vector de posición entre los puntos $A(0, 0, 0.4)$ y $B(0.2, 1.2, 0.4)$ .

El vector posición es:

$\vec{r}_{AB} = (B - A) = (0.2 \hat{i} + 1.2 \hat{j} + (0.4 - 0.4) \hat{k}) = (0.2 \hat{i} + 1.2 \hat{j}) \, m$

Ahora, tenemos que calcular el producto cruzado entre el vector posición $\vec{r}_{AB}$ y la fuerza $\vec{F}$ .

Sabemos que la fuerza es:

$\vec{F} = 600 \hat{i} + 300 \hat{j} - 600 \hat{k} \, N$

El momento de la fuerza respecto al punto $A$ se calcula como:

$\vec{M}_A = \vec{r}_{AB} \times \vec{F}$

Cálculo del Producto Cruzado

Para calcular el producto cruzado entre $\vec{r}_{AB} = (0.2 \hat{i} + 1.2 \hat{j}) \, m$ y $\vec{F} = (600 \hat{i} + 300 \hat{j} - 600 \hat{k}) \, N$ , desglosamos el cálculo:

$\vec{M}_A = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 0.2 & 1.2 & 0 \\ 600 & 300 & -600 \end{vmatrix}$

Calculamos el determinante por componentes:

– Componente $\hat{i}$ :

$M_A^i = (1.2)(-600) - (0)(300) = -720 \, N \cdot m$

– Componente $\hat{j}$ :

$M_A^j = (0)(600) - (0.2)(-600) = 120 \, N \cdot m$

– Componente $\hat{k}$ :

$M_A^k = (0.2)(300) - (1.2)(600) = -660 \, N \cdot m$

Por lo tanto, el momento de la fuerza es:

$\vec{M}_A = (-720 \hat{i} + 120 \hat{j} - 660 \hat{k}) \, N \cdot m$

Así, el momento de la fuerza con respecto al punto $A$ es:

$\vec{M}_A = (-720 \hat{i} + 120 \hat{j} - 660 \hat{k}) \, N \cdot m$

Fórmulas y Teoremas Clave

1. Leyes de Newton

Primera Ley de Newton (Ley de la Inercia): Un cuerpo permanece en reposo o en movimiento rectilíneo uniforme si la suma de las fuerzas que actúan sobre él es cero.

Segunda Ley de Newton (Ley de la Aceleración): La aceleración de un objeto es directamente proporcional a la fuerza neta aplicada e inversamente proporcional a su masa. $F = ma$

Tercera Ley de Newton (Acción y Reacción): A cada acción corresponde una reacción de igual magnitud y dirección opuesta.

2. Momento de una Fuerza

Diagrama explicativo del momento de fuerza

Fórmula: $\vec{M} = \vec{r} \times \vec{F}$ , donde $\vec{r}$ es el vector de posición y $\vec{F}$ es el vector fuerza.

3. Producto Vectorial

Fórmula básica: $\vec{A} \times \vec{B} = |A| |B| \sin(\theta) \hat{n}$ , donde $\theta$ es el ángulo entre los vectores $A$ y $B$ , y $\hat{n}$ es un vector unitario perpendicular al plano que contiene a $A$ y $B$ .

Fórmula usando una determinante:

$\vec{A} \times \vec{B} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ A_x & A_y & A_z \\ B_x & B_y & B_z \\ \end{vmatrix}$

Donde $A_x$ , $A_y$ , $A_z$ son las componentes del vector $\vec{A}$ y $B_x$ , $B_y$ , $B_z$ son las componentes del vector $\vec{B}$ .

4. Teorema de Pitágoras en 3D

Fórmula: $r = \sqrt{r_x^2 + r_y^2 + r_z^2}$ , donde $r_x$ , $r_y$ , y $r_z$ son las componentes del vector de posición en los ejes $x$ , $y$ , y $z$ .

5. Ley de los Senos y Cosenos

Ley de los Senos: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Ley de los Cosenos: $c^2 = a^2 + b^2 - 2ab\cos(C)$