Un Estudio Elemental del conjunto ℝ
Un Estudio Elemental del conjunto RTabla de Contenidos
Contents
1. Introducción
2. Definición axiomática de R
2.1. Suma o adición en R
2.2. Axiomas de la Suma en R
2.3. Multiplicación o Producto en R
2.4. Axiomas de la Multiplicación en R
2.5. Axiomas de Orden en R
3. El Axioma de Sustitución
4. Axioma de la Distributividad
5. Igualdad para la Adición
6. Igualdad en la Multiplicación
7. Propiedad Cancelativa de la Adición
8. Propiedad Cancelativa de la Multiplicación
9. Sustracción de Números Reales
10. División de Números Reales
11. Definición del conjunto N a partir de R
12. Ejercicios Resueltos (paso a paso)
12.1. Ejercicio Explicativo 01
12.2. Ejercicio Explicativo 02
12.3. Ejercicio Explicativo 03
12.4. Ejercicio Explicativo 04
12.5. Ejercicio Explicativo 05
12.6. Ejercicio Explicativo 06
12.7. Ejercicio Explicativo 07
12.8. Ejercicio Explicativo 08
12.9. Ejercicio Explicativo 09
12.10. Ejercicio Explicativo 10
13. Enlaces externos
Introducción
1. IntroducciónEl sistema de los números reales que utilizamos hoy en día es el resultado de miles de años de reflexión y descubrimiento por parte de la humanidad. Desde los inicios de nuestra civilización, ya se conocían los números enteros positivos, como 1, 2, 3, y así sucesivamente. Incluso, en épocas tan antiguas como el 300 A.C., los egipcios utilizaban números tan grandes como 100,000.
Los antiguos egipcios y babilonios desarrollaron la aritmética utilizando estos números enteros positivos, lo que les permitió realizar operaciones como la adición y la multiplicación. Sin embargo, la división era un concepto que aún no se había desarrollado por completo. Estos pueblos también comenzaron a utilizar fracciones, lo que dio origen a los números racionales (números que pueden expresarse como el cociente de dos enteros).
Los babilonios, en particular, tuvieron un gran éxito en el desarrollo de la aritmética y el álgebra gracias a su avanzada notación numérica, que, aunque tenía una base de 60 en lugar de 10, era mucho más efectiva que la de los egipcios. De hecho, una buena notación es fundamental para el desarrollo de las matemáticas.
Nuestro sistema decimal actual, que utilizamos para los números, fue creado por los indios y llegó a Europa Occidental en el siglo XII a través de la traducción de textos árabes. Sin embargo, su aceptación no fue inmediata, y tomó mucho tiempo para que se adoptara de manera generalizada. Incluso los números negativos no fueron plenamente aceptados hasta finales del siglo XVI, cuando se empezaron a considerar seriamente en el contexto de las ecuaciones matemáticas.
A diferencia de la geometría griega, que se desarrolló principalmente con fines intelectuales, el desarrollo del cálculo requirió una base lógica sólida para los números irracionales, como ,
,
Esta fundamentación lógica se logró hacia finales del siglo XIX.
Hoy en día, tenemos un sistema de axiomas que describe completamente los números reales, y a partir de estos axiomas, podemos deducir todas las propiedades de los números reales. Este enfoque es similar al método utilizado en la Geometría Euclidiana, donde se parte de ciertos axiomas o postulados para probar todos los teoremas de la geometría.
Definición axiomática de R
2. Definición axiomática de RLos números reales pueden definirse de manera formal en términos de sus propiedades y estructuras algebraicas y ordenadas. A continuación, se presentan algunos enfoques básicos para definir los números reales.
Se llama sistema de los números reales a un conjunto denotado por , provisto de:
$\quad$• Dos operaciones: Suma y multiplicación
,
$\quad$• Una relación de orden denotada por , y
$\quad$• El axioma del supremo,
los cuales se detallan a continuación:
Operación de Suma o adición de números reales
2.1. Suma o adición en R| . | |||
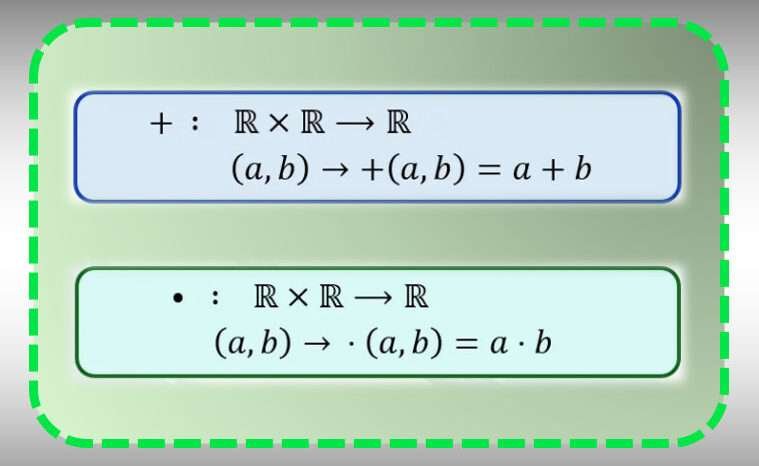
| $ (\bm{+})\,:$ | $\bm{\RR \times \RR }$ | $\bm{ \to }$ | ....$\bm{\RR}$ |
| $\bm{ (a,b) }$ | $\bm{ \mapsto }$ | $\bm{ +(a,b) = a + b }$ | |
| . |
la cual verifica los siguientes axiomas:
Axiomas de la Suma en R
2.2. Axiomas de la Suma en R| A1. Cerradura: | |
| A2. Conmutatividad: | |
| A3. Asociatividad: | $\bm{\forall\,a, b, c \in \RR \Rightarrow (a + b) + c = a + (b + c)}$ |
| A4. Identidad Aditiva: | |
| A5. Opuesto Aditivo: |
Estos axiomas de adición también se les conoce como propiedades de Clausura, Conmutativa, Distributiva, Asociativa, Elemento Neutro Aditivo y Elemento Inverso Aditivo; respectivamente
Multiplicación o Producto de números reales
2.3. Multiplicación o Producto en R| . | ||||
| • | : | $\bm{\RR \times \RR }$ | $\bm{ \to }$ | ....$\bm{\RR}$ |
| $\bm{ (a,b) }$ | $\bm{ \mapsto }$ | $ \text{•}\,\bm{(a,b) = a \!\cdot\! b }$ | ||
| . |
que verifica los siguientes axiomas:
Axiomas de la Multiplicación en R
2.4. Axiomas de la Multiplicación en R| M1. Cerradura: | |
| M2. Conmutatividad: | |
| M3. Asociatividad: | $\bm{\forall\,a, b, c \in \RR \quad \Rightarrow \quad (a \cdot b) \cdot c = a \cdot (b \cdot c)}$ |
| M4. Identidad .......Multiplicativa: | |
| M5. Opuesto .......Multiplicativo: |
Estos axiomas de multiplicación también se les conoce como propiedades de Clausura, Conmutativa, Distributiva, Asociativa, Elemento Neutro Multiplicativo y Elemento Inverso Multiplicativo; respectivamente.
Axiomas de Orden en R
2.5. Axiomas de Orden en R| O1. Tricotomía: | $\bm{\forall \,a, b \in \RR}$, una Y SOLO UNA de las relaciones .............................. se cumple: .............................. && \smash{\bm{a < b \quad,\quad a = b \quad,\quad b < a}} && |
| O2. Transitividad: | &&\text{Si: } \bm{a < b \;\,\wedge\;\, b < c \quad\Rightarrow\quad a < c}&& |
| O3. Monotonía .......de la adición: | &&\text{Si: } \bm{a < b \quad\Rightarrow\quad a + c < b + c}&& |
| O4. Monotonía de la .......multiplicación: | &&\text{Si: } \bm{a < b \;\,\wedge\;\, c > 0 \quad\Rightarrow\quad a\cdot c < b\cdot c}&& |
.
Observación 1. [Sumandos y factores]
- En
, a los números
y
se les llamará sumandos, y al número
suma de
y
- En
, a los números
y
se les llamará factores, y al número
producto de
y
El Axioma de Sustitución
3. El Axioma de SustituciónSi
El axioma de sustitución es crucial porque garantiza la consistencia y coherencia del sistema numérico. Es fundamental para la lógica y el razonamiento matemático, permitiendo que las operaciones y transformaciones en expresiones sean válidas siempre que se respete la igualdad.
Este axioma, aunque simple en su formulación, es esencial para la validez de muchos otros teoremas y operaciones en matemática, ya que asegura que las igualdades se puedan manejar de manera consistente en diversas situaciones.
Axioma de la Distributividad}
4. Axioma de la DistributividadPara toda terna de números reales
$\quad$ a) Distributiva Izquierda. && \smash{\boxed{\bm{a \cdot (b + c) = a \cdot b + a \cdot c }}} && $\quad$ b) Distributiva Derecha. && \smash{\boxed{\bm{(a + b) \cdot c = a \cdot c + b \cdot c }}} &&
La propiedad distributiva es una de las propiedades fundamentales de las operaciones aritméticas en el conjunto de los números reales. Es una propiedad que relaciona la multiplicación con la adición (y también con la sustracción), y establece cómo estas operaciones interactúan entre sí.
Igualdad en la Adición
5. Igualdad para la AdiciónPara toda terna de números reales
| Paso | ......Acción...... | Justificación |
|---|---|---|
| 1°) | por hipótesis | |
| 2°) | propiedad reflexiva | |
| 3°) | 1°), 2°) y el Claim 1 |
La propiedad de la igualdad para la adición en los números reales es un principio que describe cómo la adición afecta el orden entre los números. Esta propiedad establece que, si agregamos el mismo número a ambos lados de una desigualdad, la desigualdad original se mantiene.
Igualdad para la Multiplicación
6. Igualdad en la MultiplicaciónPara toda terna de números reales
| Paso | ......Acción...... | Justificación |
|---|---|---|
| 1°) | por hipótesis | |
| 2°) | propiedad reflexiva | |
| 3°) | 1°), 2°) y el Claim 1 |
La propiedad de igualdad para la multiplicación en los números reales describe cómo la multiplicación afecta el orden entre los números. A diferencia de la adición, la multiplicación tiene un comportamiento más complejo en relación con las desigualdades, ya que el signo del número por el que multiplicamos influye en el resultado.
Propiedad Cancelativa de la Adición
7. Propiedad Cancelativa de la AdiciónSean los números reales
| Paso | ...................Acción................... | Justificación |
|---|---|---|
| 1°) | por hipótesis | |
| 2°) | 1°) y el Remark 1 | |
| 3°) | 2°) y el axio. | |
| 4°) | 3°) y el axio. | |
| 5°) | 4°) y el axio. |
La propiedad cancelativa en la adición de los números reales es un principio fundamental que nos dice que, bajo ciertas condiciones, podemos «cancelar» o eliminar un término común de ambos lados de una igualdad sin alterar la veracidad de la igualdad.
Propiedad Cancelativa de la Multiplicación
8. Propiedad Cancelativa de la MultiplicaciónSean los números reales
| Paso | ..............Acción.............. | Justificación |
|---|---|---|
| 1°) | por hipótesis | |
| 2°) | 1°) y el Remark 2 | |
| 3°) | 2°) y | |
| 4°) | 3°) y | |
| 5°) | 4°) y |
La propiedad cancelativa en la multiplicación de los números reales es un principio fundamental que nos permite eliminar un factor común de ambos lados de una ecuación multiplicativa, siempre y cuando el factor no sea cero. Esta propiedad es esencial para simplificar y resolver ecuaciones que involucran multiplicación.
En el sistema de los números reales $\RR$ tanto la resta como la división se definen en términos de la suma y la multiplicación, respectivamente, debido a la estructura algebraica que subyace a este conjunto, que es la de un cuerpo. Un cuerpo es una estructura algebraica con dos operaciones binarias, la adición y la multiplicación, que satisfacen ciertas propiedades axiomáticas.
Sustracción de Números Reales
9. Sustracción de Números RealesPara cualquier par de números reales
La razón para definir la resta de esta manera es que en un cuerpo, la operación primaria definida es la adición, junto con la existencia de un opuesto aditivo para cada número. Esto asegura que la resta no es una operación independiente, sino una aplicación de la suma en combinación con el opuesto aditivo.
División de Números Reales
10. División de Números RealesPara cualquier par de números relaes
Al igual que la resta, la división se define a partir de la multiplicación y el inverso multiplicativo porque la multiplicación es la operación primaria, y la estructura del cuerpo asegura que para cada número real no nulo , existe un inverso multiplicativo
.
las definiciones de resta y división en el sistema de números reales como sumas y productos con los inversos respectivos reflejan la estructura algebraica del cuerpo (\RR\) y además proporcionan un marco consistente y universal para realizar operaciones aritméticas en este sistema.
Definición de los números naturales a partir de los reales
11. Definición del conjunto N a partir de RLo números naturales se construyen de manera rigurosa a partir de los elementos identidad de
, es decir comenzando con 0 y 1.
Cada número natural subsecuente se define en términos de sumas repetidas del número 1.
- 0: Es el número inicial y elemento identidad aditivo.
- 1: Es el primer número natural, definido axiomáticamente.
- 2: Se define como
.
- 3: Se define como
, es decir:
- 4: se define como
, es decir:
- Y así sucesivamente cada número natural
se construye sumando
veces el
Esta construcción asegura que todos los números naturales y sus propiedades estén bien definidos por «heredarlas» del sistema axiomático de los números reales.
Ejercicios Resueltos (paso a paso)
12. Ejercicios Resueltos (paso a paso)Ejercicio Explicativo 01
12.1. Ejercicio Explicativo 01| Paso | ..........Acción............... | Justificación |
|---|---|---|
| 1°) | Axioma | |
| 2°) | Remark 1 (igualdad para la adición) | |
| 3°) | Claim 1 (sustituyendo: | |
| 4°) | Claim 2 (distributiva izquierda) | |
| 5°) | Definition 4 (número natural 2) | |
| 6°) | Axioma |
Ejercicio Explicativo 02
12.2. Ejercicio Explicativo 02| Paso | ............Acción....................... | Justificación |
|---|---|---|
| 1°) | Axioma | |
| 2°) | ........... | Axioma |
| 3°) | ........... | Axioma |
| 4°) | ........... | Axioma |
| 5°) | ........... | Claim 2 (distributiva) |
| 6°) | ........... | Axioma |
| 7°) | ........... | Axioma |
| 8°) | ........... | Axioma |
Ejercicio Explicativo 03
12.3. Ejercicio Explicativo 03....En efecto:
| Paso | ............Acción..................... | Justificación |
|---|---|---|
| 1°) | Axioma | |
| 2°) | ..................... | Claim 2 (distributiva) |
| 3°) | ..................... | Axioma |
| 4°) | ..................... | Por el Exercise 2 |
Ejercicio Explicativo 04
12.4. Ejercicio Explicativo 04| Paso | ..............Acción...................... | Justificación |
|---|---|---|
| 1°) | Axioma | |
| 2°) | Axioma | |
| 3°) | 1°), 2°) y el Claim 1 | |
| 4°) | 3°), |
Ejercicio Explicativo 05
12.5. Ejercicio Explicativo 05| Paso | ............Acción....................... | Justificación |
|---|---|---|
| 1°) | Por el Exercise 3 | |
| 2°) | ........... | Por |
| 3°) | ........... | Por |
| 4°) | ........... | por el Exercise 3 en (3°) |
| 5°) | ........... | Por |
| 6°) | por el Exercise 4 en 5° |
Ejercicio Explicativo 06
12.6. Ejercicio Explicativo 06| Paso | ............Acción....................... | Justificación |
|---|---|---|
| 1°) | Por el Exercise 3 para | |
| 2°) | ........... | Por |
| 3°) | ........... | Por el Exercise 3 para |
| 4°) | Por el Exercise 3 para | |
| 5°) | ........... | Por |
| 6°) | ........... | Por |
| 7°) | ........... | Por |
| 8°) | ........... | Por el Exercise 3 para |
| 9°) | Por |
Ejercicio Explicativo 07
12.7. Ejercicio Explicativo 07| Paso | ............Acción................ | Justificación |
|---|---|---|
| 1°) | Definition 2 (Sustracción en | |
| 2°) | ............ | Claim 2 (distributiva) |
| 3°) | ............ | Por el Exercise 6 |
| 4°) | Definition 2 (Sustracción en |
Ejercicio Explicativo 08
12.8. Ejercicio Explicativo 08| Paso | ........Acción........ | Justificación |
|---|---|---|
| 1°) | Por | |
| 2°) | Definition 3 (División en R) |
Ejercicio Explicativo 09
12.9. Ejercicio Explicativo 09| Paso | ................Acción............................ | Justificación |
|---|---|---|
| 1°) | Por | |
| 2°) | por | |
| 3°) | .................. | 2°) y |
| 4°) | .................. | 3°) y |
| 5°) | .................. | 4°) y |
| 6°) | de 2°) y 5°) | |
| 7°) | de 1°) y 6°) (Claim 1, sustitución) | |
| 8°) | 7°) y Remark 4 (cancelativa) |
Ejercicio Explicativo 10
12.10. Ejercicio Explicativo 10| Paso | ................Acción | Justificación |
|---|---|---|
| 1°) | Por Definition 3 | |
| 2°) | 1°) y | |
| 3°) | $\frac{a}{b} + \frac{c}{d} = (a \cdot d) \cdot (b^{-1} \cdot d^{-1}) + (b \cdot c) \cdot (b^{-1} \cdot d^{-1})$ | 2°) y |
| 4°) | 3°) y el Exercise 9 | |
| 5°) | 4°) y el Claim 2 | |
| 6°) | 5°) y la Definition 3 |
Enlaces externos
13. Enlaces externosPara una mayor comprensión de los axiomas de los números reales, recomiendo los siguientes sitios de confianza, que incluyen ejercicios y demostraciones similares.
- Consulta este tutorial de cálculo de la Universidad de Chile para más detalles sobre los números reales y sus propiedades, entre otros temas interesantes.
- Consulta esta lectura sobre números reales en Alfaomega, una editorial reconocida en la publicación de libros técnicos y educativos, que amplía las demostraciones y ejercicios mencionados en este artículo.
